Motore in corrente continua
Un motore in corrente continua è costiuito da:
Uno statore a magnete permamente
Un rotore in ferro sul quale sono presenti degli avvolgimenti ed è la parte che ruota. È detto anche armatura.
Il commutatore si occupa di commutare il verso della corrente per sostenere la rotazione stabilendo un collegamento tra rotore e spazzole
Le spazzole sono collegate alla fonte di alimentazione
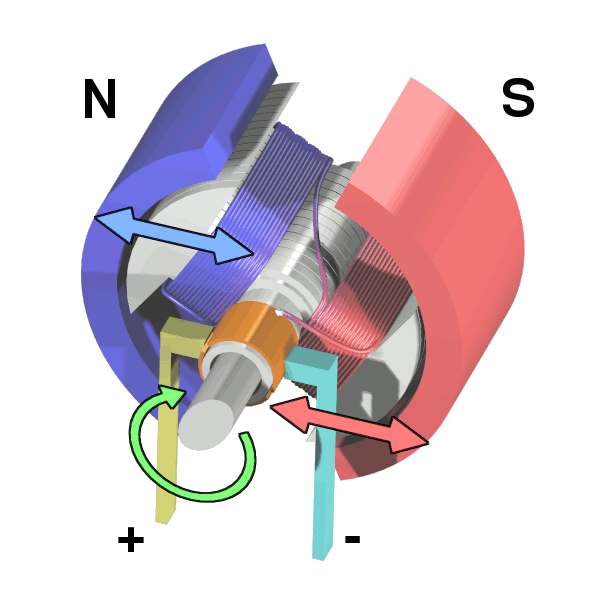
Motore in CC Wapcaplet CC BY-SA 3.0
Un motore in corrente continua può essere rappresentato elettricamente dal seguente circuito:
Circuito equivalente del motore in CC
dove \(V_{A}\) è la tensione applicata all’armatura, \(R\) è la resistenza delle spire, \(L\) è l’induttanza delle spire. \(E_{C}\) rappresenta la forza controelettromotrice che si oppone alla tensione di armatura quando il motore ruota.
Trascurando l’induttanza \(L\) che a regime si comporta come un cortocircuito, otteniamo la seguente equazione alla maglia:
\[V_{A} = R \cdot I + E_{C}\]
Si può dimostrare che la forza controelettromotrice è legata alla velocità angolare di rotazione \(\omega\) tramite una costante \(K_{E}\) detta costante elettrica che dipende dal flusso magnetico e dal numero di spire dell’avvolgimento.
\[E_{C} = K_{E} \cdot \omega\]
e dunque l’equazione diventa:
\[V_{A} = R \cdot I + K_{E} \cdot \omega\]
La coppia motrice del motore \(C\) è data dalla relazione:
\[C_{M} = K_{T} \cdot I\]
dove \(K_{T}\) è la costante meccanica del motore ed ha lo stesso valore, ma unità di misura diversa.
Funzionamento a vuoto
Supponiamo che il motore sia inizialmente fermo, dunque la sua velocità angolare \(\omega\) vale 0 e non sia applicato alcun carico al rotore. Se viene applicata una tensione \(V_{A}\) ai capi dell’armatura, si ottiene una corrente \(I_{S}\), detta corrente di spunto che vale:
\[I_{S} = \frac{V_{A}}{R}\]
e si ha una coppia \(C_{S}\) detta coppia di spunto che vale:
\[C_{S} = K_{T} \cdot I_{S} = K_{T} \cdot \frac{V_{A}}{R}\]
A causa di questa coppia, il motore inizia a ruotare con velocità angolare \(\omega(t)\) variabile nel tempo e quindi viene generata una forza controelettromotrice che si oppone alla tensione di alimentazione:
\[E_{C}(t) = K_{E} \cdot \omega(t)\]
Dopo un certo periodo di tempo \(T_{A}\), il motore raggiungerà la velocità angolare di regime \(\omega_{0}\) detta anche velocità a vuoto.
In assenza di carico, ovvero di coppia resistente, si avrà che la forza controelettromotrice avrà raggiunto il valore della tensione di alimentazione, azzerando la corrente \(I\).
\[E_{C} = V_{A} \rightarrow V_{A} = K_{E} \cdot \omega_{R} \rightarrow \omega_{0} = \frac{V_{A}}{K_{E}}\]
Essendo la corrente di regime \(I_{R}\) = 0, si ha che la coppia motrice va a zero:
\[C_{0} = K_{T} \cdot I_{0} = 0\]
Nella realtà, questa situazione non può verificarsi, in quanto sono sempre presenti attriti e perdite magnetiche. Per tale motivo, vi è una corrente \(I_{0} \neq 0\) dato che la coppia motrice deve compensare la coppia resistente.
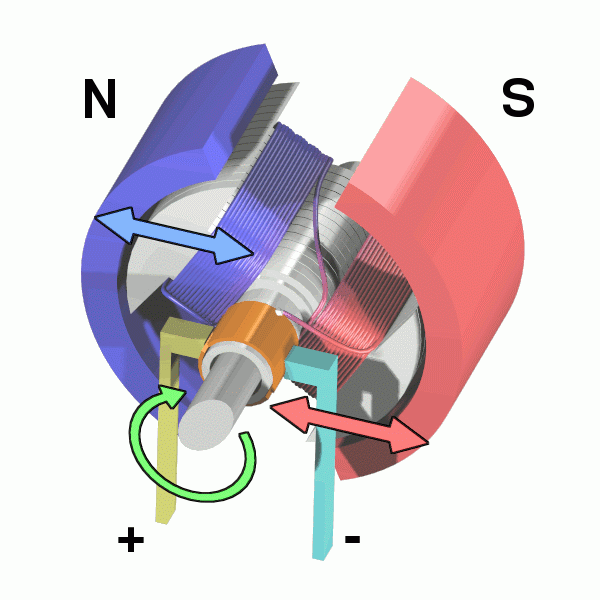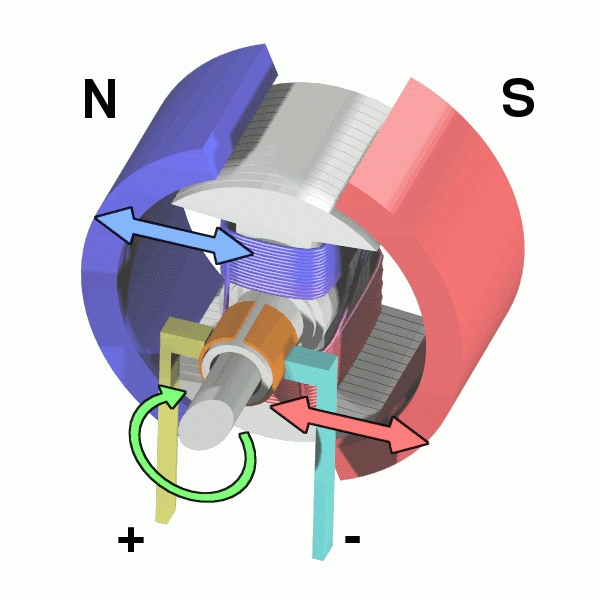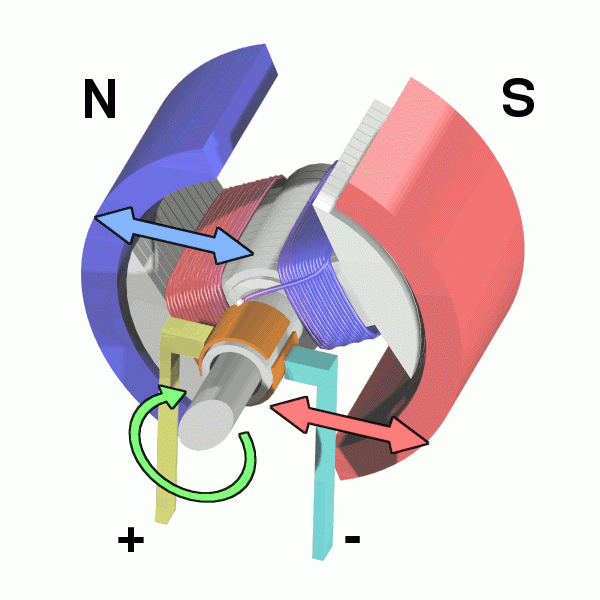
Motore in CC Abnormaal CC BY-SA 3.0
Funzionamento sotto carico
Se all’albero del motore viene applicata una coppia contraria al verso di rotazione \(C_{L}\) detta coppia resistente o frenante, la velocità angolare \(\omega\) diminuisce e viene a circolare una corrente:
\[I = \frac{V_{A} - K_{E} \cdot \omega}{R}\]
Tale corrente, produce una coppia motrice che a regime sarà uguale alla coppia resistente \(C_{M} = C_{L}\). Dato che:
\[I = \frac{C_{L}}{K_{T}}\]
Dall’equazione alla maglia, abbiamo:
\[E_{C} = V_{A} - R \cdot I = V_{A} - R \cdot \frac{C_{L}}{K_{T}}\]
Se la posto di \(E_{C}\) sostituiamo \(K_{E} \cdot \omega\), otteniamo:
\[\omega = \frac{V_{A}}{K_{E}} - R \cdot \frac{C_{L}}{K_{T}^{2}}\]
Sostituendo \(\omega_{0}\) dall’equazione:
\[H = \frac{R}{K_{T}^{2}}\]
otteniamo:
\[\omega = \omega_{0} - C_{L} \cdot H\]
\(H\) è detta costante motore ed è un indice di qualità del motore. Più piccolo è \(H\), minore sarà la perdita di velocità angolare a parità di coppia resistente.
Modello dinamico
I motore in corrente continua è un sistema dinamico caratterizzato da due costanti di tempo:
la costante di tempo elettrica \(\tau_{e}\)
\[\tau_{e} = \frac{L}{R}\]
la costante di tempo meccanica \(\tau_{m}\)
\[\tau_{m} = \frac{R \cdot J}{K_{T} \cdot K_{E}}\]
dove \(J\) è il momento di inerzia complessivo del motore collegato al carico.
La funzione di trasferimento del motore in corrente continua, nel funzionamento a vuoto, può essere quindi espressa come:
\[G(s) = \frac{\Omega(s)}{V_{A}(s)} = \frac{\frac{1}{K_{E}}}{\left( 1 + s \cdot \tau_{m} \right) \cdot \left( 1 + s \cdot \tau_{m} \right)}\]
e generalmente si ha che \(\tau_{m} \gg \tau_{e}\).